约定

$x$作为一个样本时，是列向量，$X_{n\times d}$，n行d维列向量，代表n个样本/数据。

第二章 模型评估与选择

错误率：$E=\frac{a}{m}$，精度：$acc=1-E$

在训练集误差：训练误差 or 经验误差； 新样本误差：泛化误差 (generalization error)

过拟合over（无法避免）、欠拟合under

2.2 评估方法

使用测试集测试对新样本的判别能力，使用测试误差作为泛化误差近似。 问题==> 如何选择测试集

（1）留出法 hold-out

直接把数据集$D$ 划分为互斥的两个集合：训练集S和测试集T，在S学习、用T评估。

要保持数据分布一致性，可以采用 分层采样 (stratified sampling)，进行多次随机划分、重复评估后取平均。

（2）交叉验证法 cross validation

把D划分为k个大小相似的互斥子集，然后每次k-1训练1验证，称为“k折交叉验证”，一般k=10。

如果k=m，即每个集合就一个样本，称为 留一法。这种方法的实际评估结果和直接用D训练很接近，但是计算所花成本太大（m轮）。

（3）自助法 bootstrapping

自助采样：bootstrap Sampling为基础，对D，每次随机挑选一个样本放入D’，并放回D，取m次，得到D’。

可能多次出现同一个样本。一个样本在m次采样不被采到的概率为$(1-\frac{1}{m})^{m}$，m足够大时为1/e，大约0.368。

取D’为训练集，D\D’作测试集。

在数据集小、难以有效划分训练/测试集时有用，但是改变初始数据集的分布，引入了估计偏差

（4） 调参

超参数和模型内参数。

测试数据 vs 验证集（validation set），后者其实是之前D中分出来的T，而前者是训练好以后实际使用中遇到的数据。

2.3 性能度量

衡量模型泛化能力的评价标准。

回归任务最常用：MSE均方差
$$
E(f;D)=\frac{1}{m}\sum_{i=1}^{m}(f(\bold{x_i})-y_i)^2
$$

（2）precision、recall、F1

对于二分类问题，有四种情况：TP、FP、TN、FN（预测值和真实值分别为真/假）

则有 查准率P (precision) $P=\frac{TP}{TP+FP}$， 查全率R (recall) $R=\frac{TP}{TP+FN}$，分别代表预测值为True中预测对的比例、真实值为True中被成功预测对的比例。

混淆矩阵 confusion matrix，就是四种情况的2*2表格

	预测为真	预测为假
真实为真	TP	FN
真实为假	FP	TN

PR曲线：P为纵轴，R为横轴的图，P和R一般此增彼降。

使用平衡点（P=R）可以判断一个模型的优良，越大越好；但是更好的方法是F1 score，其定义为P和R的调和平均
$$
\frac{1}{F1}=\frac{1}{2} \cdot (\frac{1}{P} + \frac{1}{R})
$$
所以$F1=\frac{2PR}{P+R}$

以及多个二分类matrix时，先各自计算PR再平均得到marco-P、marco-R和marco-F1；先加权平均得到TP、FP、TN、FN的平均再算，得到的P，R，F1是micro的。

（3） ROC & AUC

ROC， recceiver operating characteristic，受试者工作特征曲线。纵轴为 真正例率（True Positive Rate，TPR=(TP)/(TP+FN)），横轴为假正例率(FPR=FP/(TN+FP))。

真实训练中测试样例有限，所以设置分类阈值从小到大，使分类结果变化（比如提升threshold让原来False变成True，从而横纵坐标变化画出b图）

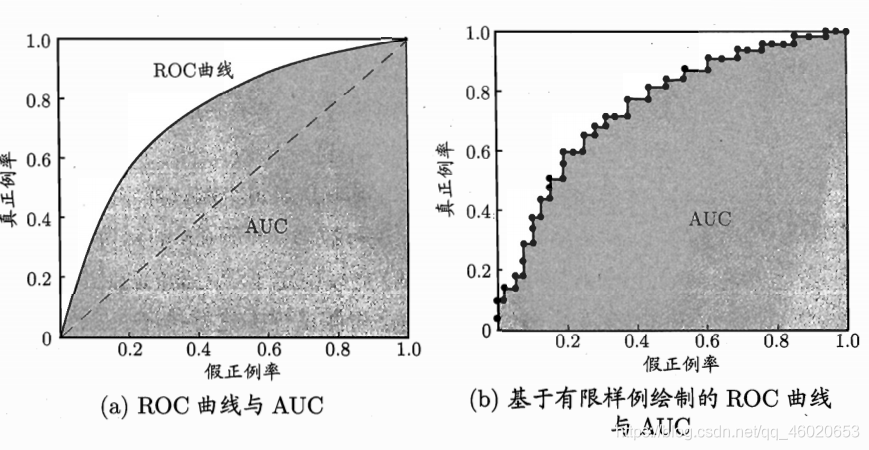
AUC： Area Under ROC Curve，就是面积，越大越好呗，

loss定义为1-AUC

（4） 代价敏感错误率、代价曲线

FP和FN的错误代价可能不对等，所以这个时候就要设定一个代价矩阵:

令$cost_{ij}$代表将第i类样本预测为第j类的代价。所以算E的时候，就要加上这个参数，以二分类为例：
$$
E=\frac{1}{m}(\sum_{\mathbf{x_i}\in D^+} II(f(\mathbf{x_i}) \neq y_i)\times cost_{01}+\sum_{\mathbf{x_i}\in D^-}II(f(\mathbf{x_i}) \neq y_i)\times cost_{10})
$$
D+和D-分别为正例集和反例集。

第三章 线性模型

$$
f(\pmb{x})=\pmb{w}^T\pmb{x}+b
$$

其中$\pmb{w}=(w_1,w_2,…,w_d)$

简单、可解释性高。

3.2 线性回归

linear regression

对于一维变量的情况下，

使用最小二乘法，即求解w和b使均方差E最小：

得到

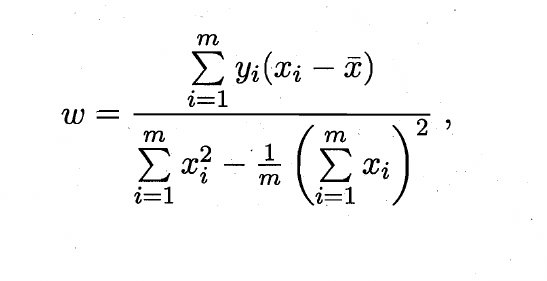
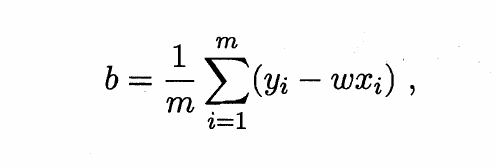
具体推导其实就是把w和b相互带进去然后代数运算，没有什么太多技巧。

广义线性模型

即使得$y=\pmb{w^Tx}+b$ 左侧的y形式发生一些变化，比如变成lny，这样就出现了非线性的关系。一般地，可以总结为：

对于单调、可微函数$g(·)$ , 令$y=g^{-1}(\pmb{w^Tx}+b)$，便称之为广义线性模型，g称为联系函数。

3.3 对数几率回归

定义

把回归任务改为分类任务的时候，从最一般的二分类任务考虑，把连续值映射到{0,1}离散值，分段函数比较好，不过这样很难连续（尤其是有突变的时候）

所以**对数几率函数 (logistic function)**出现了：
$$
y=\frac{1}{1+e^{-z}}
$$
其中z为预测值，$z= \pmb{w^Tx}+b$，其形状类似S型，属于一种Sigmoid函数。代入后整理可得到
$$
ln(\frac{y}{1-y})=\pmb{w^Tx}+b
$$
左侧的y/1-y可以看成 是/不是 的一种可能性的比值，所以这个函数叫“对数几率函数”，logit。

参数估计

要想要知道$w$和$b$，可以通过极大似然估计的方法，即（给定w、b、x_i情况下）
$$
l(\pmb{w},b)=\sum_{i=1}^m ln~p(y_i | \pmb{x_i};\pmb{w},b)
$$
最大化L函数即可，具体数学运算待补充。

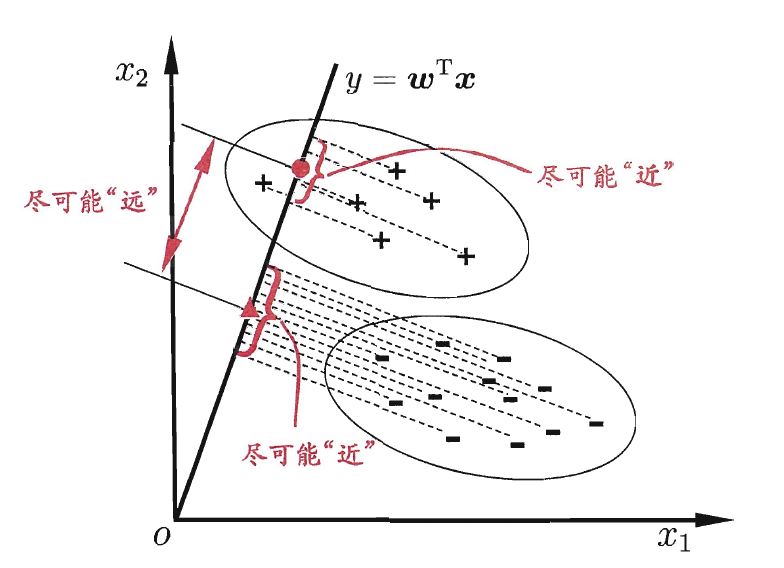
3.4 线性判别分析 LDA

LDA, Linear Discriminant Analysis，也称为Fisher判别分析。

思路简单，对于分类问题，找一条线使得同类别的样本在线上投影近、不同类尽量远；对于新样本，只需要根据投影位置判断类别即可。

第五章 神经网络 - unfinished

5.1 神经元模型

神经元、激活函数（sigmoid）基础概念，略

5.2 感知机与多层网络

线性可分 linearly separable

存在一个超平面（线性方程）能把两类样本分开，逻辑或、与、非都是线性可分问题，异或则不是。

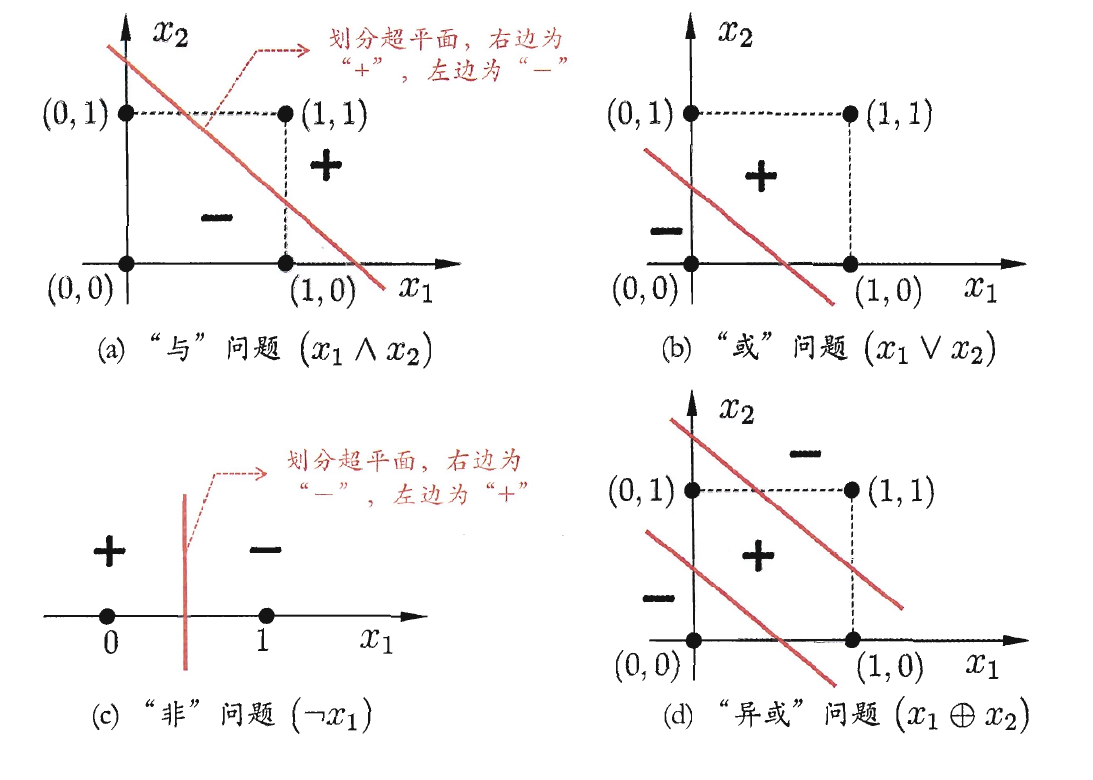
当然，可以通过增加一层（两层感知机）来解决线性不可分的异或：

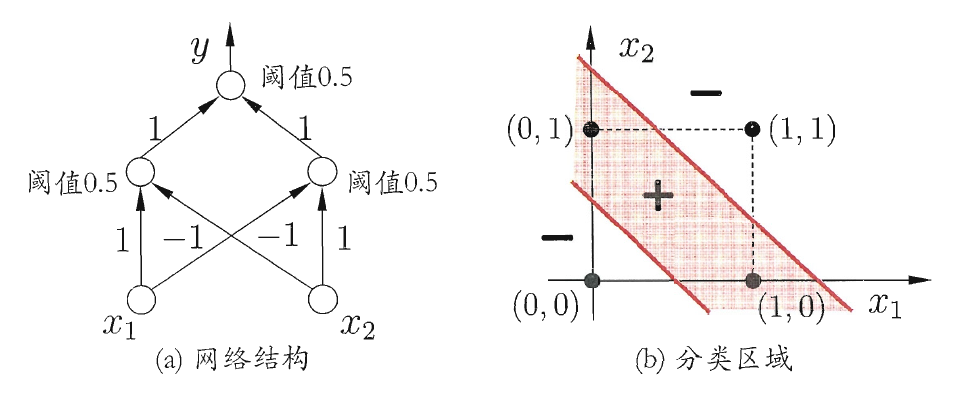
多层前馈神经网络

multi-layer feedforward neural networks, 只向前反馈信息，没有循环和反馈。

5.3 反向传播 BP

西瓜书里面叫做误差逆传播。

第六章 支持向量机 - unfinished

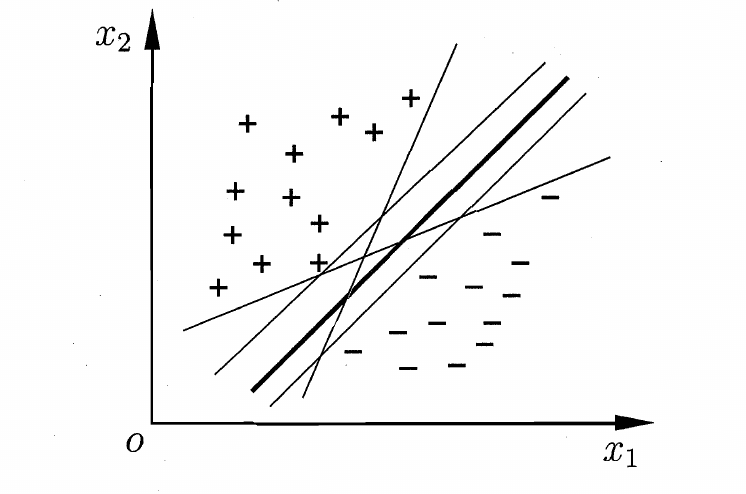
支持向量机，SVM，原理朴素，以最简单的二分类来距离，即找出一个超平面（二维就是一条直线），划分开两类“点”。显然满足条件的超平面可能有很多个（如图），我们想找看起来最好的（其实就是对于新增样本误判可能性相对更低，鲁棒性强），即图中加粗的线。他的特点就是，两类点集中距离平面最短的距离最大。

上面是一个比较通俗、不严格的解释，这里给出稍微严谨的数学定义。对于超平面，可以通过$\pmb{w^Tx}+b=0$ 这样一个方程来描述，其中$\pmb{w}=(w_1;w_2;…;w_d)$是法向量，$b$为位移项，则任意点到该平面距离$r = \frac{|\pmb{w^Tx}+b|}{||\pmb{w}||}$

定义间隔 (margin) 为$\gamma = \frac{2}{||\pmb{w}||}$，其实是人为地缩放了$\pmb{w},b$ 使得两边最近的点（带入使得等号成立）使得带入$\pmb{w^Tx}+b$后，一类结果为+1，另一类为-1，距离就是两倍的$\frac{1}{||\pmb{w}||}$。

现在要做的就是找到能使得$\gamma$一个最大的超平面，即最小化$||\pmb{w}||$

补充 需要动笔的数学问题

1. 线性回归部分，P55的数学推导，矩阵求导等
2. logit回归，极大似然估计w和b的部分。P59

---

• ← Previous Post
• Next Post →

---

---