本节内容包括训练前的一些事情:数据处理、初始化
数据预处理
一、 Zero-center
每个维度的数据,都减去均值,使得新数据的中心迁移到原点。
二、Normalization
所有维度归一化,数值范围近似相等。
- 第一种方法:先zero-centered,然后每个维度除以标准差
- 第二种方法:每个维度归一化,使得max和min是1和-1
三、PCA
筛选一些更有区分度的特征,比如协方差矩阵中,方差很小的特征(理解为对区分不同样本意义不大的特征),留下更“有用”的特征,实现数据降维。
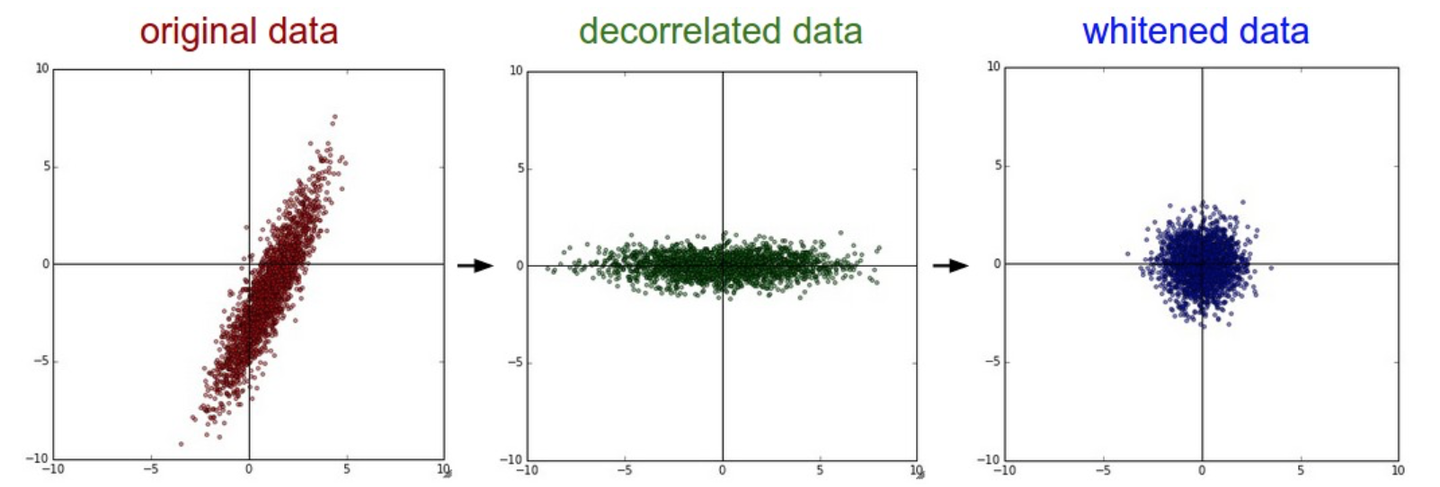
四、白化 Whitening
使各个特征的范围相同(统一尺度)、去除相关性。
几何上来看就是数据在各个方向伸缩,使其符合高斯分布(正态分布)
常见问题
预处理的时候,只能从训练集取平均!即先分训练集、验证集和测试集,然后再在训练集的基础上进行数据预处理;如果是先统一进行预处理(比如取全部数据集的mean,然后在训练集上减),就是错的!应该是训练集基础上取mean,然后所有集都减这个mean。
权重初始化
W最开始初始化,如果全零初始化,可能会导致梯度的对称性,那么就失去了意义,因为既然一开始都一样,那么正向、反向传播的时候,得到的梯度都是一样的。而且全是0也不利于梯度的传播,可能就直接消失了。另外,初始化权重大,梯度就大,对学习率要求更加敏感;权重小了,又会造成梯度消失。
一、随机初始化
根据上面的分析,我们可以通过初始化一些接近0但不为0的权重,破除对称性。
考虑到小的权重可能导致的梯度消失问题,我们使用$\frac{1}{\sqrt{n}}$来对方差进行校准,即
1 | W = np.random.randn(n)/sqrt(n) |
这种初始化调整中,假设了X和W的平均值为0(即$E[x_i]=E[w_i]=0$),在比如ReLU中输出的内容,其E显然不为0,此时一般使用$\frac{1}{\sqrt{n/2}}$,即使用
1 | np.random.randn(n)*sqrt(2.0/n) |
二、稀疏初始化 Sparse init
先初始化为全0,然后为了打破对称性,随机选择一些神经元和下一层随机连接(非全连接层),然后权重随机。
三、偏置的初始化 (init for bias)
因为W打破了非对称性,所以可以把b初始化为0。不过也可以初始化为0.01这种,使得ReLU一开始就激活,能保存、传播一些梯度。但是不一定能真正提高性能。
四、 BN
连接层(FC或卷积层)与激活函数之间,增加一个BN层。使得激活训练前,符合标准高斯分布N (0,1)。可以增强初值不好网络的鲁棒性。
正则化 regularization
控制神经网络容量,防止过拟合。
一、L2正则化
即$\frac{1}{2}\lambda \omega^2$
二、L1正则化
$\frac{1}{2}\lambda|\omega|$
三、最大范式约束
要求$||\omega||_2<c$,一般c取3或4,学习率过高时,网络也不会数值爆炸。
四、dropout
按照一定概率p,对神经元进行随机失活(或者激活),在MLP那一节里面有所介绍。
关于损失函数
普通的损失函数,在面对很多类的时候,普通softmax可能就过拟合、计算复杂度过高、内存消耗大。
分层softmax
将标签分解为一棵树——每个标签为树上一个路径,然后分类器就决策在树上向左还是向右。但是树的结构对结果影响大,且需要具体问题具体分析。
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !