一、架构分析
1. 架构概览
在本节中,将对最后一次迭代(hw3)的项目进行分析,先在此简单描述一下我的思路:
- 解析并存储自定义函数(UDF)
- 去除输入表达式空格和\t,递归地进行字符串替换掉函数调用
- 对2中得到的表达式边解析边化简,得到最终表达式
- 输出结果
因此整体架构可以被分为两部分:解析、预处理部分 以及 存储、化简部分,前者对应Parser、Lexer、UDF相关类,后者对应Expr、Term、Factor等相关类。
在最终的架构中,我从存算分离架构调整为了存算一体的架构,但本质上,解析和化简功能还是可以分开的。下面将分别进行介绍。
2. 项目架构-类图
该类图中省略了一些基本的内容,主要体现类之间的关系和一些核心功能的实现:
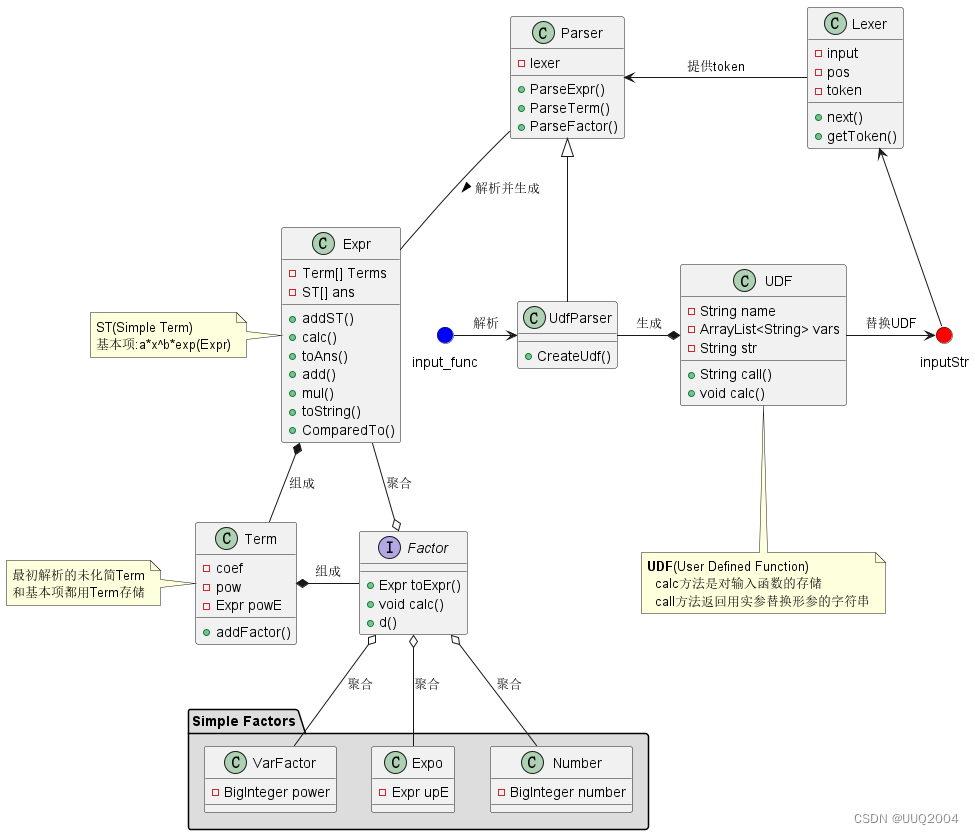
3. 类设计思路阐释
(1) 预处理和整体思路
对于Parser、Lexer部分的设计和training提供的思路类似,即使用递归下降的方法,通过Lexer对字符串进行token提取,由Parser对token进行识别和解析,完成存储,这里就不过多展开。
对于UDF(函数)的存储,设计了UDF类,
为了对UDF输入进行解析,设计了UdfParser类,实际上和Parser关联不强,只是也使用了Lexer进行token分割和提取,对于自定义函数进行名称、形参、表达式的识别和存储,生成UDF。
(2) 存储&计算
这部分是比较核心的地方,大架构参考training的Expr-Term-Factor的三层结构,设计Factor接口让Expr完成implement,以实现表达式套表达式的括号嵌套。
Factor接口定义了因子的三个共同行为,分别是求导、转换为表达式、化简,共有四个实现,即Number(常量)、VarFactor(对应x^a)、Expr(表达式因子)、Expo(对应exp())
每个底层因子都很直观地按照形式化表述的定义设计,通过calc和toExpr和d这三个接口中规定的方法,把add和mul都通过Expr类进行实现,减少了实现其他类之间加&乘运算的代码量。
4. 用数据说话——基于统计结果的分析
使用IDEA插件Statistic,得到各个类的规模(代码行数、方法个数)
| Class | Source Code Lines | 方法个数 |
|---|---|---|
| Factor | 5 | 3 |
| UdfParser | 25 | 3 |
| Number | 25 | 6 |
| Expo | 28 | 6 |
| VarFactor | 29 | 6 |
| Lexer | 43 | 5 |
| Udf | 46 | 5 |
| Term | 87 | 12 |
| MainClass | 80 | - |
| Parser | 136 | 9 |
| Expr | 301 | 16 |
可以看到Expr类的代码行数最多,因为Expr不仅是最终得出答案的最大容器,同时也是因为架构设计时,对于不同Factor的加乘运算都在Expr进行(使用toExpr后mul,或者使用Expr的addST)。
方法数量较多是因为对于每种Factor或Term、Expr,都设计了多种构造函数,虽然可能看起来比较冗余,但是这样易于扩展,使得代码可读性增强。例如在VarFactor的构造函数就有传入int类、传入BigInteger类的两种构造函数。
使用IDEA插件Metric Reloaded,分别计算出各个方法的圈复杂度
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Expo.Expo(Expr) | 0 | 1 | 1 | 1 |
| Expo.Expo(Factor) | 0 | 1 | 1 | 1 |
| Expo.calc() | 0 | 1 | 1 | 1 |
| Expo.d() | 0 | 1 | 1 | 1 |
| Expo.getUp() | 0 | 1 | 1 | 1 |
| Expo.toExpr() | 0 | 1 | 1 | 1 |
| Expr.Expr() | 3 | 2 | 2 | 2 |
| Expr.Expr(Factor) | 3 | 2 | 2 | 2 |
| Expr.add(Expr) | 1 | 1 | 2 | 2 |
| Expr.addST(Term) | 7 | 1 | 4 | 5 |
| Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| Expr.calc() | 10 | 3 | 5 | 7 |
| Expr.compareTo(Expr) | 0 | 1 | 1 | 1 |
| Expr.copy() | 1 | 1 | 2 | 2 |
| Expr.d() | 1 | 1 | 2 | 2 |
| Expr.isFactor() | 8 | 6 | 7 | 9 |
| Expr.mul1(Expr) | 16 | 6 | 6 | 7 |
| Expr.toAns() | 34 | 4 | 15 | 18 |
| Expr.toAnsFir() | 28 | 4 | 11 | 11 |
| Expr.toAnsIn() | 2 | 1 | 2 | 2 |
| Expr.toExpr() | 0 | 1 | 1 | 1 |
| Expr.toString() | 3 | 2 | 3 | 4 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.getRem() | 0 | 1 | 1 | 1 |
| Lexer.getToken() | 0 | 1 | 1 | 1 |
| Lexer.next() | 6 | 2 | 5 | 6 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| MainClass.pre(String) | 48 | 8 | 13 | 17 |
| Number.Number(int) | 0 | 1 | 1 | 1 |
| Number.Number(int, BigInteger) | 0 | 1 | 1 | 1 |
| Number.calc() | 0 | 1 | 1 | 1 |
| Number.d() | 0 | 1 | 1 | 1 |
| Number.getValue() | 0 | 1 | 1 | 1 |
| Number.toExpr() | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.getLexer() | 0 | 1 | 1 | 1 |
| Parser.parseDX() | 0 | 1 | 1 | 1 |
| Parser.parseEF() | 8 | 4 | 6 | 6 |
| Parser.parseEP() | 3 | 1 | 3 | 3 |
| Parser.parseExpr() | 8 | 1 | 7 | 7 |
| Parser.parseFactor() | 11 | 5 | 7 | 8 |
| Parser.parseTerm(int) | 3 | 1 | 4 | 4 |
| Parser.parseVF() | 3 | 1 | 3 | 3 |
| Term.Term() | 0 | 1 | 1 | 1 |
| Term.Term(BigInteger, BigInteger, Expr) | 0 | 1 | 1 | 1 |
| Term.Term(Factor) | 4 | 1 | 4 | 4 |
| Term.addFactor(Factor) | 5 | 1 | 5 | 5 |
| Term.addPow(BigInteger) | 0 | 1 | 1 | 1 |
| Term.calc() | 1 | 1 | 2 | 2 |
| Term.d() | 1 | 1 | 2 | 2 |
| Term.getFlag() | 0 | 1 | 1 | 1 |
| Term.getPow() | 0 | 1 | 1 | 1 |
| Term.getPowE() | 0 | 1 | 1 | 1 |
| Term.mulFlag(BigInteger) | 0 | 1 | 1 | 1 |
| Term.mulFlag(int) | 0 | 1 | 1 | 1 |
| Udf.Udf(String, ArrayList |
0 | 1 | 1 | 1 |
| Udf.calc() | 7 | 4 | 5 | 6 |
| Udf.call(ArrayList |
4 | 1 | 3 | 3 |
| Udf.getName() | 0 | 1 | 1 | 1 |
| Udf.getNum() | 0 | 1 | 1 | 1 |
| UdfParser.CreateUdf() | 1 | 1 | 2 | 2 |
| UdfParser.UdfParser(Lexer) | 0 | 1 | 1 | 1 |
| UdfParser.UdfParser(Lexer, HashMap<String, Udf>) | 0 | 1 | 1 | 1 |
| VarFactor.VarFactor(BigInteger) | 0 | 1 | 1 | 1 |
| VarFactor.VarFactor(int) | 0 | 1 | 1 | 1 |
| VarFactor.calc() | 0 | 1 | 1 | 1 |
| VarFactor.d() | 1 | 2 | 1 | 2 |
| VarFactor.getPow() | 0 | 1 | 1 | 1 |
| VarFactor.toExpr() | 0 | 1 | 1 | 1 |
| compare(Pair<BigInteger, Expr>, Pair<BigInteger, Expr>) | 2 | n/a | n/a | n/a |
可以看到圈复杂度高的方法主要有Main的pre方法、Expr的两个toAns方法和Expr的mul1方法,pre方法解析str中的自定义函数、两个toAns方法是最终输出(第一项和其他项),因此有很多分支。mul1方法实现了两个Expr的乘法,涉及判0和一些其他事宜,复杂度较高,而其他方法圈复杂度都小于10,整体复杂性可以接受。
而对于每个Class,我们也有:
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Expo | 1 | 1 | 6 |
| Expr | 3.89 | 15 | 70 |
| Lexer | 2.2 | 6 | 11 |
| MainClass | 7.5 | 13 | 15 |
| Number | 1 | 1 | 6 |
| Parser | 3.56 | 7 | 32 |
| Term | 1.75 | 5 | 21 |
| Udf | 2 | 4 | 10 |
| UdfParser | 1.33 | 2 | 4 |
| VarFactor | 1.17 | 2 | 7 |
可以看到WMC(加权方法复杂度)同样聚集在Expr类,其次是Parser,这和架构设计和功能特性关联很强。
二、迭代
1. 架构演化
第一次作业 —— 存算分离的典型
第一次作业由于内容较少,而且training和OOLens都提供了递归下降的解读和示例,因此可能大家的设计主要分为两类——存算一体和存算分离,我最开始为了方便理清思路、便于调试,使用了后者,同时明确了使用基本项(a*x^b)和基本项构成的加法多项式存储结果。
但实际上先解析再计算架构为了区分两个过程,我认为最好设计单独的基本项和多项式类,不要在化简时直接复用解析时使用的Expr,但我觉得其实差不多所以没有分开,开发过程中确实思路上和实现时产生了一些困扰。
第二次作业 —— 缝缝补补和一些动摇
第二次作业允许了括号嵌套,新增了指数因子和自定义函数。前者实际上递归下降方法本身就支持多层括号,而新增指数因子只需要新增一个Expo类,自定义函数经过严谨论证如果不考虑效率(即函数表达式和形参的化简)直接使用字符串替换即可,因此架构只会增添,不会太改变。
但是我担心我的存算分离架构在括号过多的时候可能运行效率不佳,因此在解析表达式因子的时候也调用了Expr.calc()进行计算,但最外一层仍需要最后调用calc,此时我的架构处于一个不太明确的状态,也可能导致重复运算,但由于细节处理得当,整体运行速度允许有这样的冗余。
基本功能实现了,但是为了性能分肯定要做基本的合并同类项——这时候判断exp上面的expr是否相等就要花头脑了。为此我对Expr的存储顺序进行了规定,保证toString后结果唯一,用字符串判断。这时候由于没有单独的Poly类导致写起来确实有点麻烦。
第三次作业
第三次作业加的内容不多,就是求导和自定义函数嵌套。求导只需要先化简内部表达式或因子,在每一层都实现求导,再实现乘法规则即可,自定义函数嵌套由于字符串替换的递归实现,所以无需做出什么改变。
整体架构没有发生什么变化。
可见我的架构实际上比较清晰,类的数量较少,比较轻量级,但每个类的功能不够单一,部分类的代码量大,导致迭代和维护相对困难。
2. 迭代情景假设——三角函数
新增三角函数的话,因为cos和sin之间可以相互转化,所以只需要新增实现Factor接口的sin类,在Parser和Lexer部分相应修改。
对应的,基本项需要扩充为ax^bexp(Expr)*sin(Expr),化简仍然依靠Expr的toString比较sin里面是否相同。
三、本地测试、强测、互测和性能优化
1. 我的“Bug”们
在第一次作业中,为了实现更好的性能分,我试图将正项提前以减少一个加号,但是写的时候对于0项的处理没有弄好,之前的逻辑是在化简的时候保证0不出现,因此输出没有考虑0的部分,但是在优化了部分逻辑、新增正向提前后,前面化简的时候有个部分忘记去除了0项,导致输出错误,十分可惜。
这个惨痛的教训让我意识到:一个功能在可以做的时候就要做好,即使增加冗余也比出错好,这样就可以使自己的程序更加robust,而不是试图依赖上下游的处理,一个不小心就弄出问题。这次出现bug的方法圈复杂度较高、代码行数也高,因此很容易考虑不周到,导致一个疏忽就犯了错,但由于为了追求输出更短,其代码逻辑本身就很琐碎,因此我尝试了增加容错和冗余的方法保证正确性。
在第三次作业中,互测被卡了TLE。因为之前没考虑TLE的事情(毕竟已经边化简边解析了,不会被很简单的1-1的一堆次方卡,而且看到强测时间给的很长),所以很多可以优化效率的地方没有实现,而且增加了一些容错和冗余(比如输出前再计算一次),结果就被卡了。最终分析后,我发现在exp合并的时候,Expr的toString会花费很多时间,而实际上Expr如果不改变是不需要多次toString的,于是在对Expr的toString记忆化处理后,顺利通过bug修复。
2. 测试方法与互测
主要以跑评测机为主,随机生成数据、使用同学们的评测机等,但随机的话其实数据很弱,很难生成出bug,而且互测中即使使用评测机生成出bug数据后还需要手动化简为符合cost的结果,因此手动构造一些极端情况、边界情况的数据也很必要。
另外也会通过粗略分析对方代码架构的方式,有针对性地进行数据设计,有些同学会无脑先做n次方再进行化简,这时候1-1+x的n次方就会让他算得很多导致TLE等等。
长度优化与效率优化
上文提到过,关于长度优化,最基础的合并同类项(第二次以后通过Expr有序toString进行判断)、正项提前(这一项导致输出逻辑变得更长了,因此我特意将输出第一项单独实现了一个方法(toAnsFir),试图使得方法简单可读性强)外,没有进行额外优化(担心时间复杂度变得很坏,以及有时候提取公因数还不如不提)。
而效率优化主要是在计算前先保证内部已经化简(用change的Tag进行记忆化),以及toString的时候通过记忆化,减少了无意义的重复运算。这些优化对于各个方法复杂度几乎没有影响。
四、心得体会
OO正课相比OOpre可谓不是一个层级的,第一单元的学习也让我收获颇丰,不仅是简单的写代码速度提升,更是对于写代码之前,对于简洁高效的架构设计以及预判未来拓展方向、预留拓展空间的考量提升颇多。这一点在OOpre中只是“听到了老师有讲过”,但是没有在写代码过程中自己感受到。
另外第一次作业在实现的时候确实有一定的思维难度,不真正下手写一些感觉自己的理解都是虚无缥缈的,边写边深化自己的理解,然后再订正自己的大思路,我觉得这是适合我的方法,因此我也觉得我其实应该在第二次作业的时候进行重构,因为有了新的想法,发现自己之前的设计有缺陷,其实重构是最好的,如果有五六次作业,或者最后一次不是比较简单好实现的求导,那我肯定果断重构了。
五、建议
第一单元教程很完善,不过我觉得应该在第一次就允许括号套括号,以确保大家对递归下降法的理解比较完善准确。
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !