感觉其实没什么内容,记录一下主要是防忘
Softmax函数
$$
\pmb{\hat{y}}=softmax(\pmb{o})~\ where ~~\hat{y_j}=\frac{\exp(o_j)}{\sum_{k}\exp(o_k)}
$$
可以理解为,对于一组输出 o, 通过softmax函数将其“归一化”,如果有n个分量,那么得到的y就是这n个分量的概率分布。
这里的概率分布我理解为,满足了归一性、非负性,所以可以是一个概率分布。 即不存在因果性
Softmax回归
在普通线性回归的输出层外,增加一层softmax函数。
$$
\pmb{O}=\pmb{XW+b}\
\pmb{\hat{Y}}=softmax(\pmb{O})
$$
损失函数:交叉熵(cross-entropy Loss)
对于label y和prediction $\pmb{\hat{y}}$,损失函数l:
$$
l(y,\hat{y})=-\sum_{j=1}^{q} y_j\log \hat{y_j}
$$
因为y是独热标签,所以右侧其实只有一项为非0的,所以最小化损失函数意味着最大化对正确标签的预测(log yj-hat)
对损失函数求导:
代入softmax函数,然后把log的分子分母用除法规则拆开,就得到了第二行。
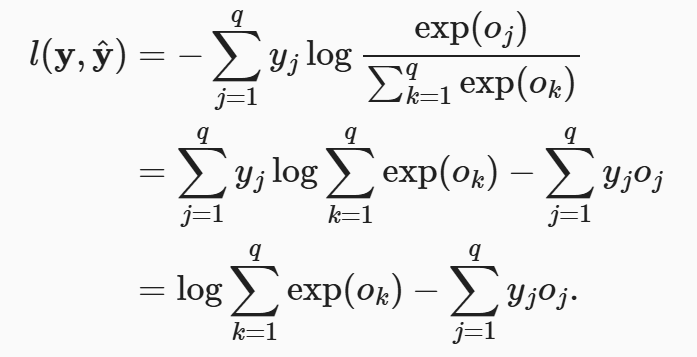
如果此时,对于一个预测$o_j$ 求偏导,那么得到一个有趣的形式:
$$
\partial _{o_j} l(\pmb{y},\pmb{\hat{y}})=\frac{\exp(o_j) }{\sum_k \exp(o_k)}-y_j=softmax(o)_j-y_j
$$
这个形式正是 预测的概率 和 标签值的差异,而且这个实际上是一个梯度(l对o的偏导,根据链式求导法则,我们关心的真正梯度$\frac{\partial l}{\part W}=\frac{\part l}{\part o} \frac{\part o}{\part W}$,前面这一项我们已经快速求出,而后面这一项,根据$O=WX+b$,实际上就是$X$。因此对于softmax,dW的计算相对简便。
注意事项
为了防止梯度爆炸或消失,让在计算梯度的时候,进行exp操作之前,先给每行的output减去行内max,保持数值稳定。进行了这个操作以后,实际测试中train_accuracy从39到了41,test_accuracy也明显增加。
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !