这篇文章提出通过层间分析法(layer-wise analysis) 实现在神经网络训练中“debug”,并解释了Batch Norm后的网络到底哪好?
概述
一、Hessian矩阵
从这里开始可能会多次混用Hessian Matrix和FIM,这两个之间有数学上的关系:数学补充
具体来讲,在训练DNN时,Hessian矩阵 或 FIM(Fisher Information Matrix)非常重要。但是计算Hessian矩阵实际上是需要很大的内存和时间,所以试图使用效率高的方法去近似,比如K-FAC算法。不过K-FAC算法有两个假设:1) weight-gradients in different layers are assumed to be uncorrelated; 2) the input and output-gradient in each layer are approximated as independent.
于是就可以成功地把full FIM表示为一个分块对角阵:$\pmb{F} = diag(F_1,…,F_K)$,其中每一个$F_k$称为sub-FIM(具体到每一层的FIM),并可通过以下公式计算/估算:
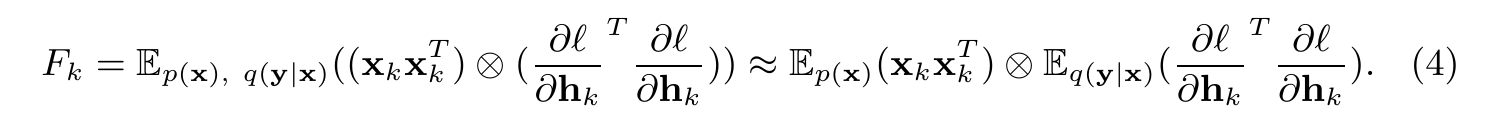
上面这个式子其实有点像文中比较开始部分中从一维线性回归的Hessian矩阵计算,到多维。其形式都是一个Covariance Matrix 然后$\otimes$ 一个东西(这个$\otimes$是Kronecker product,链接中的博客有简单介绍)
二、layer-wise条件分析的基础——从full到sub:取其精华
1. FIM的重要信息
为了让sub-FIM也能表征出full FIM能给我们的信息,首先我们要知道full FIM中哪些信息比较重要,然后再看看sub-FIM能不能也拿到这些:
其中,黑塞矩阵的两个具体特征更重要,他们分别是1. 矩阵最大特征值$\lambda_{max}$ 2. 矩阵的条件数(conditional number) $\kappa (\pmb{H})$
因为:
Property 1 :$\lambda_{max}(F_k)$indicates the magnitude of the weight-gradient in each layer, which shows the steepness of the landscape w.r.t.different layers.
Property 2 : $\kappa (F_k)$indicates how easy it is to optimize the corresponding layer.
这里的大K表示网络层数,小k表示第几层。
2. 实验
**目标:**证明sub-FIMs能反映出full FIM的信息和趋势
**任务:**MNIST
**变量:**BN 和 无BN(plained)
观察变量:某个layer(图中用了第三层和第六层)的sub-FIM和full FIM的两变量($\lambda_{max}, \kappa_{percentage}$)趋势是否有明显一致性。
注:这里的$\kappa$用的是$\frac{\lambda_{max}}{\lambda_{p}}$的定义,其中$\lambda_p$代表第p大的特征值,比如$\kappa_{100%}$其实就是条件数的最初定义。
结果(Figure 1):
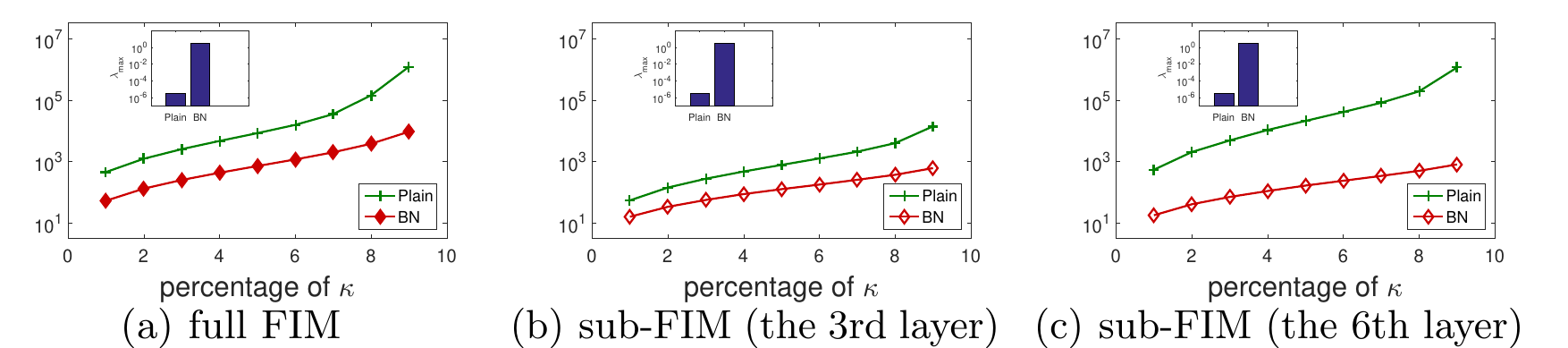
还是比较明显的,两方面结论:
- plained出现梯度消失(最大特征值1e-5),而BN组梯度就很好;BN提升了conditioning。
- 上文提出的layer-wise conditioning分析有展现网络学习动态的潜力。
3. 高效地直接计算 两个值
既然已经验证通过sub-FIMs来展现网络学习动态的能力(主要通过这两个属性),那么考虑直接高效算出这两个值,而不是先近似sub-FIM再计算。
定义:$\Sigma_{x}=\mathbb{E}{p(x)}(xx^T), \Sigma{\nabla\pmb{h}} = \mathbb{E}{q(y|x)}(\frac{\partial l}{\partial \pmb{h}}^T\frac{\partial l}{\partial \pmb{h}})$ 分别是输入的协方差矩阵、反向传播的梯度协方差矩阵,该层的sub-FIM $F=\Sigma_x \otimes \Sigma{\nabla\pmb{h}}$,则有
$$
\lambda_{max}(F)=\lambda_{max}(\Sigma_x)\cdot \lambda_{max}(\Sigma_{\nabla \pmb{h}})\
\kappa(F)=\kappa(\Sigma_x)\cdot \kappa(\Sigma_{\nabla \pmb{h}})
$$
三、BN好吗?到底怎么好?
1. BN的层间尺度不变性
在原文第四节中,使用上文的layer-wise 条件分析法,分析了BatchNorm怎么样。
首先提出了两个Theorem,描述了Normalization方法使网络具有一种“缩放不变性”。(这里有待再理解)
实验
然后就是基于实验进行分析了,同样还是MNIST,20层MLP,每层256 neurons。
变量: 1. initialization方法:random / HE-init 2. Plain / BN
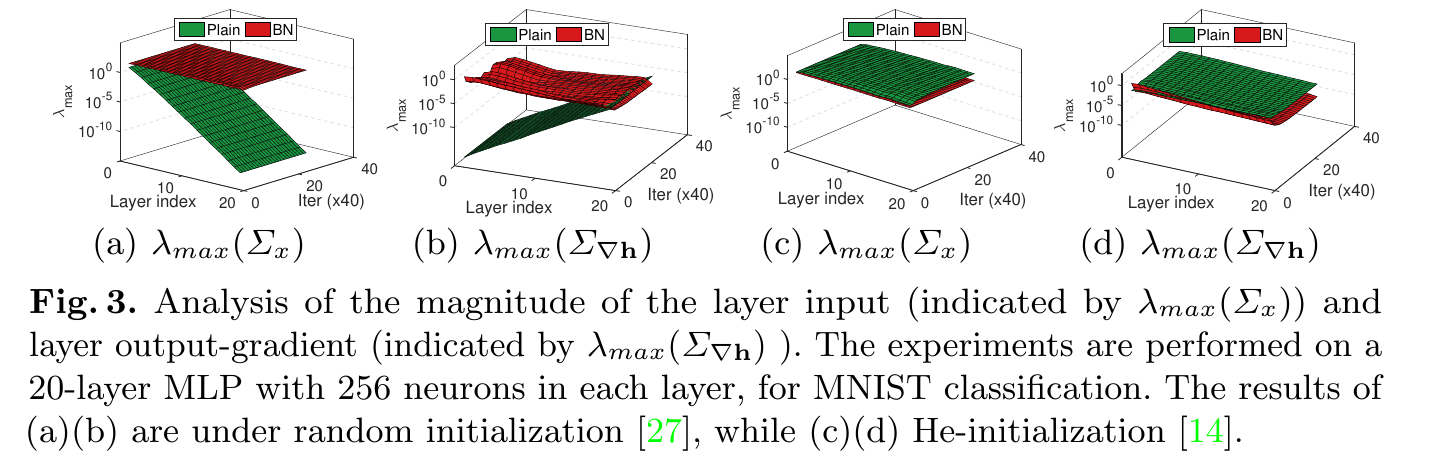
结果表明,BN能很好地维持住input/output-gradient在各层的取值,而plain就会使得这两个值指数级的下降,HE-initialization缓解了这一点。
不过我有一个问题就是,如果只是从上文的层间分析来看,我们想要得到$\lambda_{max}(F)=\lambda_{max}(\Sigma_{x})\cdot \lambda_{max}(\Sigma_{\nabla \pmb{h}})$ ,这里虽然拆开了两方向的最大特征值,发现了明显变化,但是乘起来不就抵消了吗?如果单纯只用之前的方法去算$\lambda_{max}(F), \kappa(F)$岂不是看不出什么差别???
2. Weight Domination
定义
某一层发生Weight Domination现象为:权重矩阵$W_k$、梯度$\frac{\partial L}{\partial W_k}$,有$\lambda_{max}(W_k)>> \lambda_{max}(\frac{\partial L}{\partial W_k})$,这时候的$\lambda$就只能是奇异值了。
其实这种weight domination本质上是某一层的梯度太小了,参数可能几乎不更新了,这可能是因为W的不断增加或input的不断减少(难道说这里呼应了上一节对$\lambda_{max}(F)$的拆分?)
然而,即使BN稳定了layer input,但可能也同样会因为weight的magnitude增加而表现变差。
后果&实验
Weight Domination使得网络学习能力变差,这里又做了个实验,通过禁止其权重更新的方式模拟weight domination(这对吗…)

观察到0的越多,表现越差(但是我觉得这是肯定的啊,你都不让更新权重了,有的时候可能显然是可以很好地更新的,这种模拟是否真的hold)
3. BN改善了DNN各层的条件(condition)
使用layer-wise分析方法验证“BN中的whitening input可以提升优化的条件” 这个proposition,结果发现不仅提升了每层输入的condition,还提升了梯度的condition。
另外还有 dying neurons 问题,就是ReLU以后未激活(输入小于等于0),full neurons则是对每个example都activate;猜测正是这个dying neurons导致plain组有很多小/零的eigenvalue,而BN组因为center了,所以没有什么dying/full(这里存疑啊,为什么考虑full,以及真就没dying了吗,怎么保证对所有一定都激活?猜测?)
四、 深度残差网络
本文认为,训练深度残差网络时随着层数增加,表现变差不仅仅是因为过拟合,同样也有优化困难的原因。
引入实验
ResNet实验,复现Resnet论文的实验。观察到loss先增加、再在random guess中几乎不变(weight domination),最后足够多的迭代后减小。
层间条件分析
分析最后一个线性层(交叉熵之前),观察输入的$\lambda_{max}(\Sigma_x)$,参数矩的二范式$||W||2$,和梯度协方差的$\lambda{max}$。
认为:输入x的$\lambda$大,使得梯度大,后面是W大,进而W使得loss增大(这到底是为什么。。。)
1. 解决方法
在最后一个线性层前加一个BN。
实验复现
TODO:
- 构建正确的模型结构,train方法,到底怎么写。
- 如何正确地挂上hook,以及正确算出想要的值(这些值是每层的?还是整个网络的?怎么计算)
- 画图和可视化
- 对比,以及使用两个工具。
备注
TODO:
- BP推导 和 3.2节理解
- 3.1节数学推导
- Pytorch torch.hook 学习 + 两节实验复现
- .lua文件学习
- Structure tensor? second moment matrix
Unsolved problem
- Eqn 1,2, 4到底怎么来的
- condition number到底有什么用
- 3.1节高效计算,理解proposition1
3.2节 BP,弄清楚输出梯度、输入梯度、权重梯度什么的。第四节的Theorem1和2, 以及weight domination的definition- 残差网络:定义、性质和训练。
- 如何理解第五节5.1之前那段,解释loss变化的Analysis of Learning Dynamics.
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !